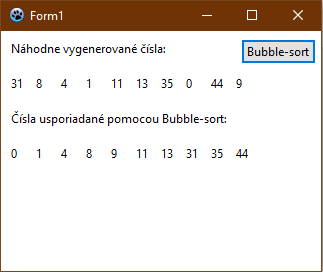
Bubble-sort
The Bubble- sort sorting, also called exchange sorting, is an algorithm that is based on comparing array elements which are placed next to each other. In ascending order, the elements change positions if the next element is smaller than the previous one. In the first step of the comparison, on the last position is the highest (largest) element in the specified array. Other elements of the array may remain at their unchanged locations, depending on the element with which they were compared. In the next steps we do not have to compare all the pairs of elements, as some of the elements could be sorted in one of the previous steps. After each step, at least one array element is arranged correctly. Now we'll show you the Bubble-sort sorting process. We have an array with eight numeric elements 4, 8, 7, 3, 5, 9, 1 and 2. The lowest value of a given array is number one and the highest value is nine. Logically, we see that the number one will be the first (left) and the number nine will be the last right. We start by comparing the first two elements (Figure 127):
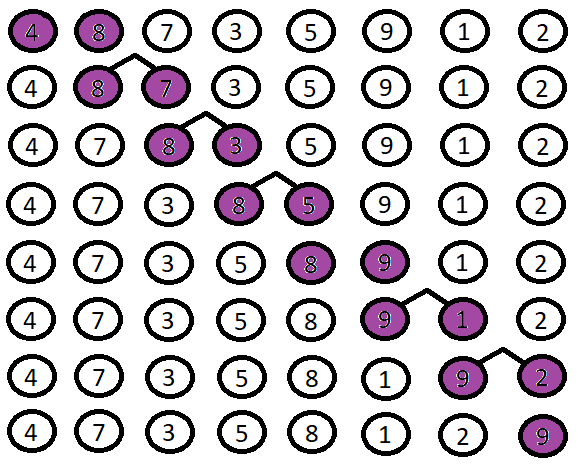
= 4<8 - the elements do not change the position
= 8<7 - the elements do change the position
= 8<3 - the elements do change the position
= 8<5 - the elements do change the position
= 8<9 - the elements do not change the position
= 9<1 - the elements do change the position
= 9<2 - the elements do change the position
= element final placement (step completed)
When the topmost element is in the last place of the array, the sorting cycle is restarted. In the figure below, we can see how each element will be sorted by value from lowest to highest each time the sort cycle is started (Figure 128).

We can see that the elements were properly aligned already at the sixth run of the cycle. However, the sorting cycle must be run once more, since it does not have to know whether the elements in the first two places are properly aligned. Therefore, sorting is started again and the correct placement of the first two elements is checked. If we calculate how many times the cycle has been run, we find that the eight-element array runs seven times, which means that for an array of elements n, the sorting cycle Bubble-sort runs n-1 times. Now let's try to program this sorting.
First, we create an array of
ten random elements, which we write on the graphical area. Then we call
the procedure BubbleSort . We have defined this so that the
procedure gradually passes through the individual elements of the array. We
just need n-1 transitions around the array. If the
current element is greater than the next, they will exchange their positions. Thus,
the cycle passes through each element sequentially, provided that if the
condition is not met, that is, the current element is smaller than the next,
the cycle memorizes the position of that element and begins the process
again. We know that if it begins to sort the rest disordered array, thus
repeated n-1 transitions (Figures 129 and 130).